-o0| At the end of having browsed in this site |0o-
Cast a vote here if you think it should move up in the Top-100 ranking:
You will be transferred to the Top-100 site, but may then return here by going "BACK"

   1.  Fixed mass (kg) (boat, oars, and fixed portion of rower). 
   2.  Moving mass (kg) of the rower (van Holst- one mass, ROWING- two 
masses). 
   3.  Blade-normal force (N) on the oar blade (Van Holst- the blade 
normal force; ROWING- the equivalent force at the oarhandle). The force is 
defined to rise and fall linearly during the stroke. 
   4.  Oar length (m) pin to blade-center-of-pressure- the outboard.
   5.  Oar shaft catch angle (rad).
   6.  Oar shaft release angle (rad).
   7.  Slide travel (m).
   8a. Free recovery period (sec) (van Holst).
   8b. Stroke rate (1/min) (ROWING).
   9.  Oar blade cant angle (rad).
  10.  Oar blade surface area (m^2).
  11.  Hull resistance factor (N-(sec/m)^2).
  12.  Blade lift and drag coefficients vs. angle of attack.
  13a. Maximum slide speed (m/s, van Holst).
  13b. Defined slide motion period fractions (ROWING).

I have made no changes to the input.

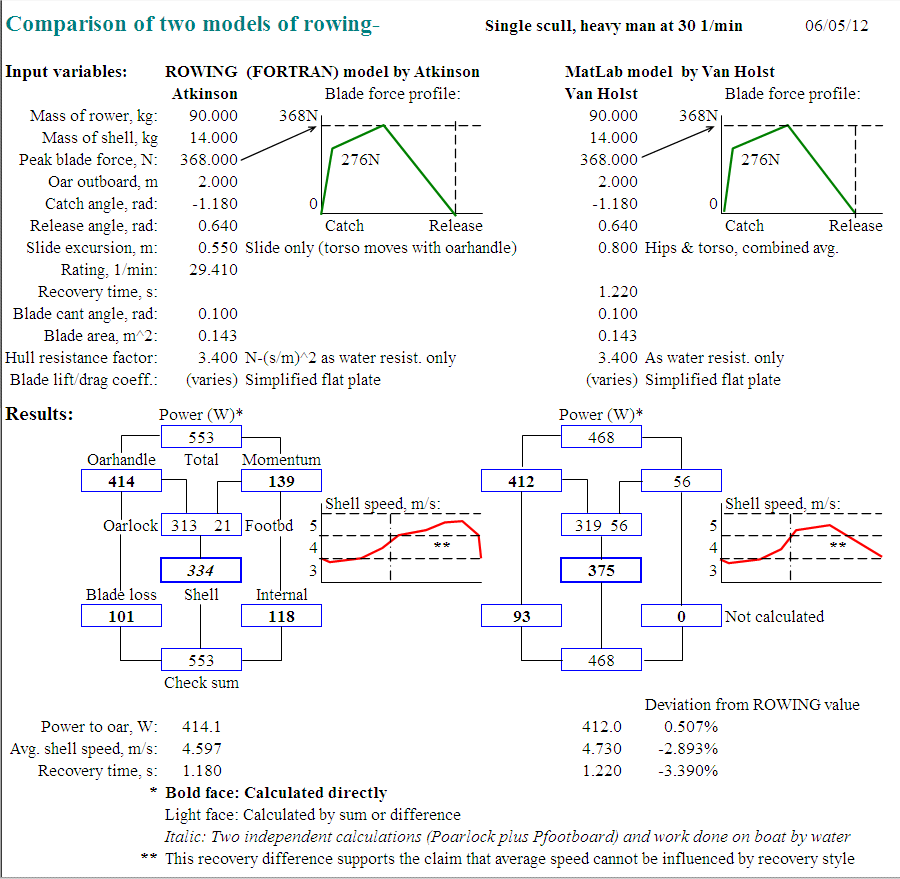Observations:
1. After nearly a decade of extensive research in this field we know of no other comparable maths models.
2. The van Holst model does not calculate the internal work lost in the body of the rower. This has no effect on the oarhandle, blade, or footboard work but does effect the definition of total rower power and the resulting system efficiency.
3. The considerable difference in the definition of the momentum in the free return supports our claim that average shell speed cannot be influenced by differences in recovery style.
4. The ROWING model has been run with different (Hoerner) oarblade lift and drag coefficients- produceing a near identical result- thus bolstering our suspicion that blade form characteristics (other than surface area (drag) and cant angle) have little effect on average shell speed.

Comment:
Heretofore no one else has calculated the zero-slip blade locus, the instantaneous blade attack angle and velocity, the instantaneous absolute blade slip (and the consequent work lost), the instantaneous forces of lift and drag, the work at the footboard (other than by V. Kleshnev of the AIS), the effect of the blade catch angle and the oarhandle force profile (other than P. Mallory) on average shell speed, and the internal work on the rower's body.

Some have challenged the validity of the results predicted by each model but no one has yet come forward with anything other than citations of the "conventional wisdom" (no numerical values offered) to argue the counter case.

See also the one-dimensional model by Cabrera, Ruina, and Kleshnev.

We feel that the time has come to take seriously the findings revealed in the exercise of comprehensive rowing models. Through the recent study of our own models we believe that more has now been revealed about the physical details of rowing than have been found heretofore over much of the previous analytical history of the sport.

Contact us:
If the subject is the model comparison please direct comment and inquiry to each of us and, if the subject is but one of the models, to each specifically.